The "You Are What You Eat" Customer Segmentation
Project Overview
Project Purpose
The purpose of this project is to segment up the customer base in order to increase business understanding, and to enhance the relevancy of targeted messaging & customer communications, using k-means clustering.
GitHub Repository Link
The source code and datasets for this project can be found at my GitHub repository.
Context
The Senior Management team from a supermarket chain client were disagreeing about how customers shopped and how lifestyle choices affected which food areas customers purchased from, or notably, did not purchase from.
They asked a consulting firm to use data and Machine Learning to segment their customers based on engagement with each major food category. This would aid the client’s understanding of their customer base and enhance the relevance of targeted messaging and customer communications.
Actions
The first step is to compile the necessary data from several database tables, namely the transactions table and the product_areas table. The relevant information is joined together using Pandas, and the transactional data is aggregated across product areas, from the most recent six months to a customer level. The final data for clustering is, for each customer, the percentage of sales allocated to each product area.
As a starting point, k-means clustering is tested and applied for this task. Some data pre-processing is required, most importantly feature scaling to ensure all variables exist on the same scale - a very important consideration for distance-based algorithms such as k-means.
As k-means is an unsupervised learning approach, in other words there are no labels - a process known as Within Cluster Sum of Squares (WCSS) is used to understand what a “good” number of clusters or segments is.
Based on this, the k-means algorithm is applied onto the product area data, the clusters are appended to the customer base, and the resulting customer segments are profiled to understand the differentiating factors.
Results
Based on iterative testing using WCSS, a customer segmentation with 3 clusters is settled on. These clusters range in size, with Cluster 0 accounting for 73.6% of the customer base, Cluster 2 accounting for 14.6%, and Cluster 1 accounting for 11.8%.
There are some extremely interesting findings from profiling the clusters.
For Cluster 0 a significant portion of spend is allocated to each of the product areas - showing customers without any particular dietary preference.
For Cluster 1 quite high proportions of spend are allocated to Fruit & Vegetables, but very little to the Dairy & Meat product areas. It could be hypothesized that these customers are following a vegan diet.
Finally customers in Cluster 2 spend significant portions within Dairy, Fruit & Vegetables, but very little in the Meat product area - so similarly, an early hypothesis is that these customers are more along the lines of those following a vegetarian diet.
To help embed this segmentation into the business, “You Are What You Eat” has been proposed as a name for the segmentation.
Growth/Next Steps
It would be interesting to run this clustering/segmentation at a lower level of product areas, so rather than just the four areas of Meat, Dairy, Fruit, Vegetables - clustering spend across the sub-categories below those categories. This would mean more specific clusters could be created, and an even more granular understanding of dietary preferences within the customer base could be obtained.
Here the focus has just been on variables directly linked to sales - it could be interesting to also include customer metrics such as distance to store, gender etc to give an even more well-rounded customer segmentation.
It would be useful to test other clustering approaches such as hierarchical clustering or DBSCAN to compare the results.
Data Overview
The primary focus is on identifying customer segments based on their transactions within the food based product areas, so only those will be selected.
The code below:
- Import the required python packages & libraries
- Import the tables from the database
- Merge the tables to tag on
product_area_namewhich only exists in theproduct_areastable - Drop the non-food categories
- Aggregate the sales data for each product area, at customer level
- Pivot the data to get it into the right format for clustering
- Change the values from raw dollars, into a percentage of spend for each customer (to ensure each customer is comparable)
# import required Python packages
from sklearn.cluster import KMeans
from sklearn.preprocessing import MinMaxScaler
import pandas as pd
import matplotlib.pyplot as plt
# import tables from database
transactions = pd.read_excel('grocery_database.xlsx', sheet_name='transactions')
product_areas = pd.read_excel('grocery_database.xlsx', sheet_name='product_areas')
# merge data on product area id
transactions = pd.merge(transactions, product_areas, how='inner', on='product_area_id')
# drop the non-food category
transactions.drop(transactions[transactions['product_area_name'] == 'Non-Food'].index, inplace=True)
# aggregate sales at customer level by product area
transactions_summary = transactions.groupby(['customer_id', 'product_area_name'])['sales_cost'].sum()
# pivot data to place product area as columns
transactions_summary_pivot = transactions.pivot_table(index='customer_id', columns='product_area_name', values='sales_cost', aggfunc='sum', fill_value=0, margins=True, margins_name='Total').rename_axis(None, axis=1)
# turn sales into % sales
transactions_summary_pivot = transactions_summary_pivot.div(transactions_summary_pivot['Total'], axis=0)
# drop the total column
data_for_clustering = transactions_summary_pivot.drop(['Total'], axis=1)
After the data pre-processing using Pandas, we have a dataset for clustering that looks like the below sample:
| customer_id | dairy | fruit | meat | vegetables |
|---|---|---|---|---|
| 2 | 0.246 | 0.198 | 0.394 | 0.162 |
| 3 | 0.142 | 0.233 | 0.528 | 0.097 |
| 4 | 0.341 | 0.245 | 0.272 | 0.142 |
| 5 | 0.213 | 0.250 | 0.430 | 0.107 |
| 6 | 0.180 | 0.178 | 0.546 | 0.095 |
| 7 | 0.000 | 0.517 | 0.000 | 0.483 |
The data is at customer level, and we have a column for each of the highest level food product areas. Within each of those we have the percentage of sales that each customer allocated to that product area over the past six months.
K-Means
Concept Overview
K-Means is an unsupervised learning algorithm, meaning that it does not look to predict known labels or values, but instead looks to isolate patterns within unlabelled data.
The algorithm works in a way where it partitions data-points into distinct groups (clusters) based upon their similarity to each other.
This similarity is most often the eucliedean (straight-line) distance between data-points in n-dimensional space. Each variable that is included lies on one of the dimensions in space.
The number of distinct groups (clusters) is determined by the value that is set for “k”.
The algorithm does this by iterating over four key steps, namely:
- It selects “k” random points in space (these points are known as centroids)
- It then assigns each of the data points to the nearest centroid (based upon euclidean distance)
- It then repositions the centroids to the mean dimension values of it’s cluster
- It then reassigns each data-point to the nearest centroid
Steps 3 & 4 continue to iterate until no data-points are reassigned to a closer centroid.
Data Preprocessing
There are three vital preprocessing steps for k-means, namely:
- Missing values in the data
- The effect of outliers
- Feature Scaling
Missing Values
Missing values can cause issues for k-means, as the algorithm won’t know where to plot those data-points along the dimension where the value is not present. If we have observations with missing values, the most common options are to either remove the observations, or to use an imputer to fill-in or to estimate what those value might be.
As we aggregated our data for each customer, we actually don’t suffer from missing values so we don’t need to deal with that here.
Outliers
As k-means is a distance based algorithm, outliers can cause problems. The main concern arises when scaling input variables, a very important step for a distance based algorithm.
The goal is to prevent any variables from clustering together due to a single outlier value, which would make it difficult to compare their values to the other input variables. Rigorous investigation of outliers is always recommended. Fortunately, in this case involving percentages, this issue is not encountered.
Feature Scaling
Again, as k-means is a distance based algorithm, meaning it relies on understanding how similar or different data points are across dimensions in n-dimensional space, the application of Feature Scaling is extremely important.
Feature Scaling forces values from different columns to exist on the same scale, enhancing the learning capabilities of the model. There are two common approaches: Standardisation and Normalisation.
Standardisation rescales data to have a mean of 0 and standard deviation of 1, with most datapoints falling between -4 and +4.
Normalisation rescales datapoints to exist between 0 and 1.
For k-means clustering, either approach is far better than no scaling. Here, normalisation will be applied to ensure all variables have the same 0 to 1 range, enabling the k-means algorithm to judge each variable in the same context. Standardisation can result in different ranges variable to variable, which is less useful here (although not always true).
Another reason to choose Normalisation is that the scaled data will all be between 0 and 1, compatible with any categorical variables encoded as 1’s and 0’s.
In this case, percentages are already between 0 and 1. Normalisation is still applied for the following reason: One product area may dominate sales, and end up dominating the clustering space. Normalising all variables will spread even smaller product areas proportionately between 0 and 1.
The code below uses MinMaxScaler from scikit-learn to apply Normalisation. A new scaled object is created because the actual percentages may make more intuitive business sense when profiling clusters later, so it’s good to have both options available.
# create scaler object
scale_norm = MinMaxScaler()
# normalise the data
data_for_clustering_scaled = pd.DataFrame(scale_norm.fit_transform(data_for_clustering), columns=data_for_clustering.columns)
Finding A Good Value For k
At this point here, the data is ready to be fed into the k-means clustering algorithm. Before that, it’s important to understand what number of clusters the data should be split into.
In the world of unsupervised learning, there isn’t a definitive right or wrong value for this. It truly depends on the data being dealt with, as well as the specific scenario in which the algorithm is being used. For our client, having a very high number of clusters might not be appropriate, as it would be too challenging for the business to grasp the nuances of each cluster in a way that allows them to apply the right strategies.
Finding the “right” value for k can feel more like an art than a science, but there are some data-driven approaches that can be helpful!
The approach being utilized here is known as the Within Cluster Sum of Squares (WCSS), which measures the sum of the squared Euclidean distances that data points lie from their closest centroid. WCSS can provide insight into the point at which adding more clusters offers little extra benefit in terms of separating the data.
By default, the k-means algorithm within scikit-learn uses k = 8, which means it aims to split the data into eight distinct clusters. The goal is to find a better value that fits the data and the task at hand.
In the code below, multiple values for k will be tested, and the changes in the WCSS metric will be plotted. As the value of k increases (in other words, as the number of centroids or clusters increases), the WCSS value will consistently decrease. However, these decreases will become smaller and smaller with each additional centroid. The aim is to identify a point where this decrease is quite noticeable before reaching a point of diminishing returns.
# set up range for search, and empty list to append wcss scores to
k_values = list(range(1,10))
wcss_list = []
# loop through each possible value of k, fit to the data, append the wcss score
for k in k_values:
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
kmeans.fit(data_for_clustering_scaled)
wcss_list.append(kmeans.inertia_)
# plot wcss by k
plt.plot(k_values, wcss_list)
plt.title('Within Cluster Sum of Square - by k')
plt.xlabel('k')
plt.ylabel('WCSS Score')
plt.tight_layout()
plt.show()
Above code gives us the below plot - which visualises our results.
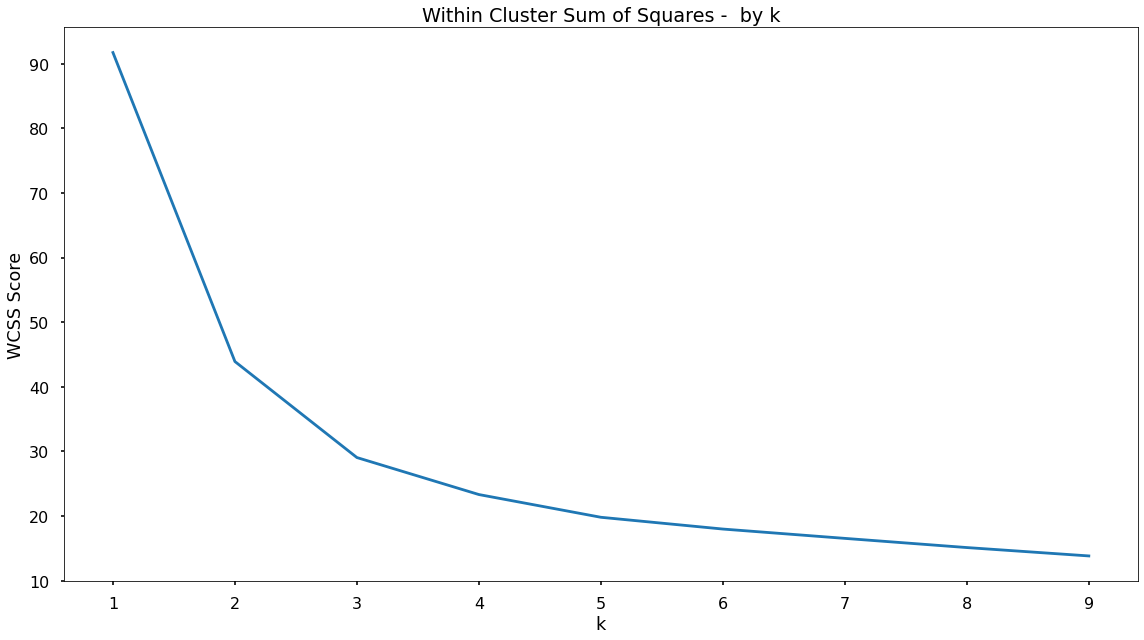
Based upon the shape of the above plot - there does appear to be an elbow at k = 3. Prior to that we see a significant drop in the WCSS score, but following the decreases are much smaller, meaning this could be a point that suggests adding more clusters will provide little extra benefit in terms of separating our data. A small number of clusters can be beneficial when considering how easy it is for the business to focus on, and understand, each - so we will continue on, and fit our k-means clustering solution with k = 3.
Model Fitting
The below code will instantiate the k-means object using a value for k equal to 3. We then fit this object to our scaled dataset to separate our data into three distinct segments or clusters.
# instantiate our k-means object
kmeans = KMeans(n_clusters = 3, random_state = 42)
# fit to our data
kmeans.fit(data_for_clustering_scaled)
Append Clusters To Customers
With the k-means algorithm fitted to the data, we can now append those clusters to the original dataset, meaning that each customer is tagged with the cluster number that they most closely fit into based upon their sales data over each product area.
In the code below, this cluster number is tagged onto the original dataframe.
# add cluster labels to the original data
data_for_clustering['cluster'] = kmeans.labels_
Cluster Profiling
Once the data is separated into distinct clusters, the client needs to understand what is driving the separation. This allows the business to comprehend the customers within each cluster and the behaviors that make them unique.
Cluster Sizes
In the below code the number of customers that fall into each cluster is assessed.
# check cluster sizes
data_for_clustering["cluster"].value_counts(normalize=True)
Running that code shows us that the three clusters are different in size, with the following proportions:
- Cluster 0:
73.6%of customers - Cluster 2:
14.6%of customers - Cluster 1:
11.8%of customers
Based on these results, there is a noticeable skew toward Cluster 0, with Cluster 1 and Cluster 2 being proportionally smaller. This isn’t a matter of right or wrong; it simply reveals pockets within the customer base that exhibit different behaviors - and this is precisely what is desired.
Cluster Attributes
To understand what these different behaviors or characteristics are, we can analyze the attributes of each cluster in terms of the variables fed into the k-means algorithm.
# profile clusters (mean % sales for each product area)
cluster_summary = data_for_clustering.groupby("cluster")[["Dairy","Fruit","Meat","Vegetables"]].mean().reset_index()
Above code results in the following table:
| Cluster | Dairy | Fruit | Meat | Vegetables |
|---|---|---|---|---|
| 0 | 22.1% | 26.5% | 37.7% | 13.8% |
| 1 | 0.2% | 63.8% | 0.4% | 35.6% |
| 2 | 36.4% | 39.4% | 2.9% | 21.3% |
For Cluster 0 we see a reasonably significant portion of spend being allocated to each of the product areas.
For Cluster 1 we see quite high proportions of spend being allocated to Fruit & Vegetables, but very little to the Dairy & Meat product areas. It could be hypothesised that these customers are following a vegan diet.
Finally customers in Cluster 2 spend, on average, significant portions within Dairy, Fruit & Vegetables, but very little in the Meat product area - so similarly, we would make an early hypothesis that these customers are more along the lines of those following a vegetarian diet.
Application
Although this is a straightforward solution, the fact that it is based on high-level product sectors will aid category managers and business executives in better understanding the client base.
Tracking these clusters over time would allow the client to more quickly react to dietary trends, and adjust their messaging and inventory accordingly.
Based on these clusters, the client will be able to target customers more accurately - promoting products and discounts to customers that are truly relevant to them - overall enabling a more customer focused communication strategy.